W jaki sposób elektrycznie naładowana cząstka zachowuje się w polach elektrycznych i magnetycznych?
Cząstka naładowana elektrycznie jest cząstkąktóry ma ładunek dodatni lub ujemny. Może to być zarówno atom, cząsteczki, jak i cząstki elementarne. Kiedy elektrycznie naładowana cząstka znajduje się w polu elektrycznym, działa na nią siła Coulomba. Wartość tej siły, jeśli znana jest wartość natężenia pola w danym punkcie, obliczana jest za pomocą następującego wzoru: F = qE.
I tak,
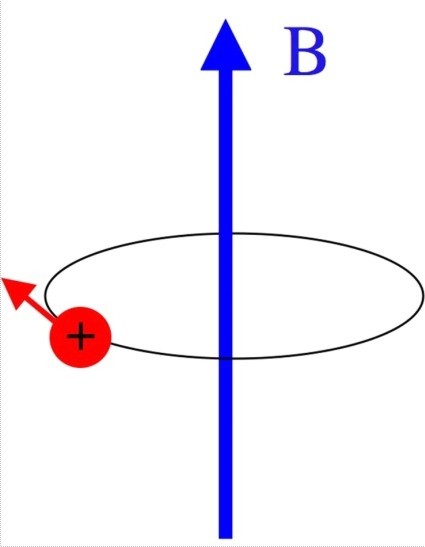
Teraz rozważ efekt Halla. Eksperymentalnie odkryto, że pole magnetyczne wpływa na ruch naładowanych cząstek. Indukcja magnetyczna jest równa maksymalnej sile, która wpływa na prędkość ruchu takiej cząsteczki od strony pola magnetycznego. Cząsteczka naładowana porusza się z prędkością jednostki. Jeśli elektrycznie naładowana cząstka leci w pole magnetyczne przy danej prędkości, siła działająca z pola będzie prostopadła do prędkości cząstki i odpowiednio do wektora indukcji magnetycznej: F = q [v, B]. Ponieważ siła oddziaływująca na cząstkę jest prostopadła do prędkości ruchu, wówczas przyspieszenie, jakie daje ta siła, również prostopadła do ruchu, jest normalnym przyspieszeniem. Odpowiednio, prostoliniowa trajektoria ruchu zostanie wygięta, gdy naładowana cząstka dostanie się do pola magnetycznego. Jeśli cząsteczka leci równolegle do linii indukcji magnetycznej, wówczas pole magnetyczne nie działa na naładowaną cząstkę. Jeśli leci prostopadle do linii indukcji magnetycznej, siła działająca na cząstkę będzie maksymalna.

Teraz piszemy prawo Newtona II: qvB = mv2/ R lub R = mv / qB, gdzie m jest masą ładunkucząstki, a R jest promieniem trajektorii. Z tego równania wynika, że cząstka porusza się w jednolitym polu wokół okręgu o promieniu. Zatem okres obrotu naładowanej cząstki wokół obwodu nie zależy od prędkości ruchu. Należy zauważyć, że w naładowanej elektrycznie cząstce uwięzionej w polu magnetycznym energia kinetyczna pozostaje niezmieniona. Z uwagi na to, że siła jest prostopadła do ruchu cząstki w dowolnym punkcie trajektorii, siła pola magnetycznego, która działa na cząstkę, nie wykonuje pracy związanej z ruchem ruchu naładowanej cząstki.

Kierunek siły działającej na ruchnaładowaną cząstkę w polu magnetycznym można określić za pomocą "zasady lewej ręki". Aby to zrobić, musisz ustawić lewą dłoń tak, aby cztery palce wskazywały kierunek prędkości naładowanej cząsteczki, cóż, linie indukcji magnetycznej są skierowane do środka dłoni, w którym to przypadku kciuk wygięty pod kątem 90 stopni wskaże kierunek działania siły, która działa pozytywnie naładowana cząstka. W przypadku, gdy cząsteczka ma ładunek ujemny, kierunek siły będzie przeciwny.
Jeśli wpadnie elektrycznie naładowana cząstkaobszar wspólnych efektów pól magnetycznych i elektrycznych, wówczas zadziała siła, zwana siłą Lorentza: F = qE + q [v, B]. W tym przypadku pierwszy termin odnosi się do komponentu elektrycznego, a drugi do komponentu magnetycznego.





